# 'vector' Dialect
[TOC]
MLIR supports multi-dimensional `vector` types and custom operations on those
types. A generic, retargetable, higher-order `vector` type (`n-D` with `n > 1`)
is a structured type, that carries semantic information useful for
transformations. This document discusses retargetable abstractions that exist in
MLIR today and operate on ssa-values of type `vector` along with pattern
rewrites and lowerings that enable targeting specific instructions on concrete
targets. These abstractions serve to separate concerns between operations on
`memref` (a.k.a buffers) and operations on `vector` values. This is not a new
proposal but rather a textual documentation of existing MLIR components along
with a rationale.
## Positioning in the Codegen Infrastructure
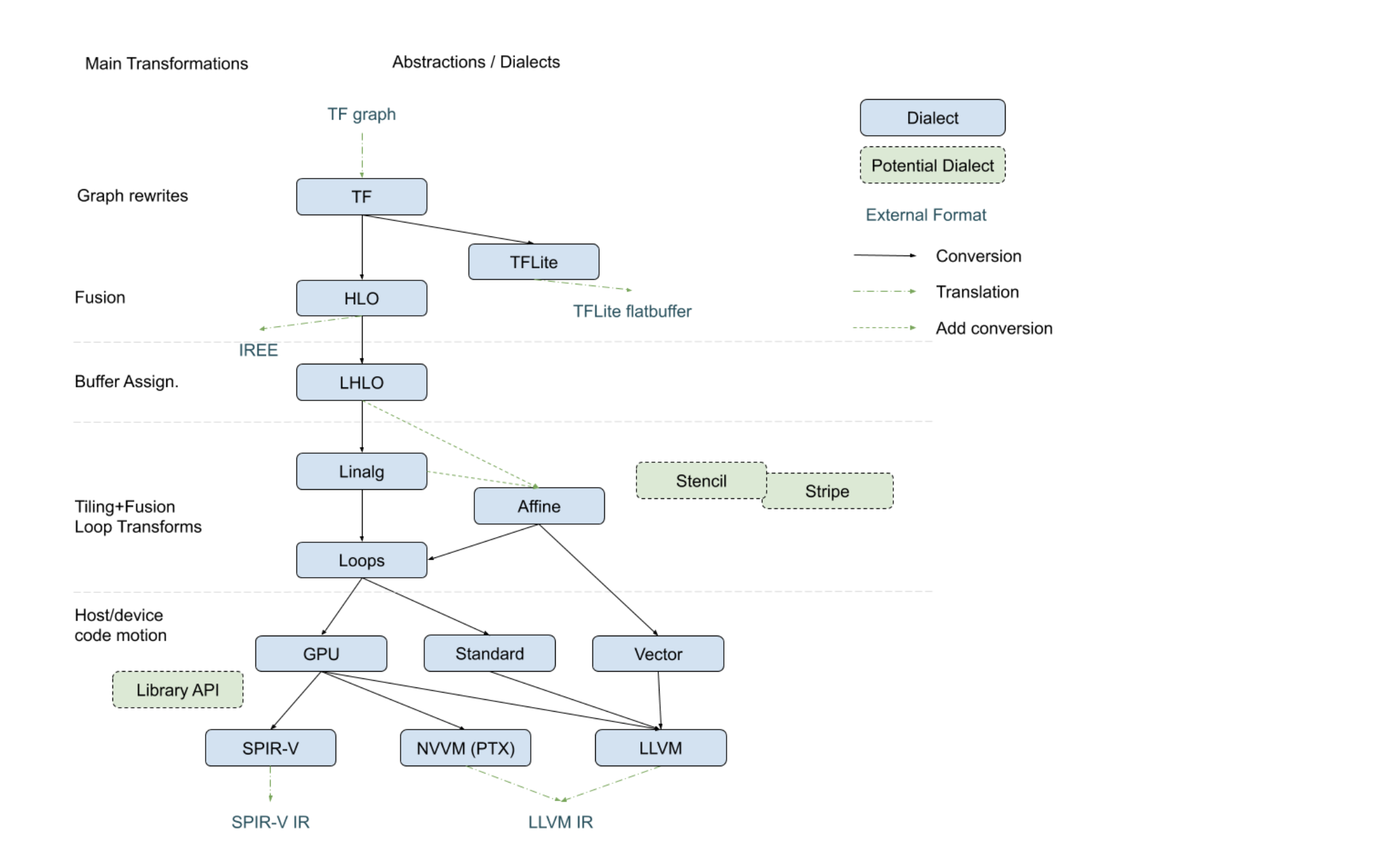
The following diagram, recently presented with the
[StructuredOps abstractions](https://drive.google.com/corp/drive/u/0/folders/1sRAsgsd8Bvpm_IxREmZf2agsGU2KvrK-),
captures the current codegen paths implemented in MLIR in the various existing
lowering paths.
The following diagram seeks to isolate `vector` dialects from the complexity of
the codegen paths and focus on the payload-carrying ops that operate on std and
`vector` types. This diagram is not to be taken as set in stone and
representative of what exists today but rather illustrates the layering of
abstractions in MLIR.
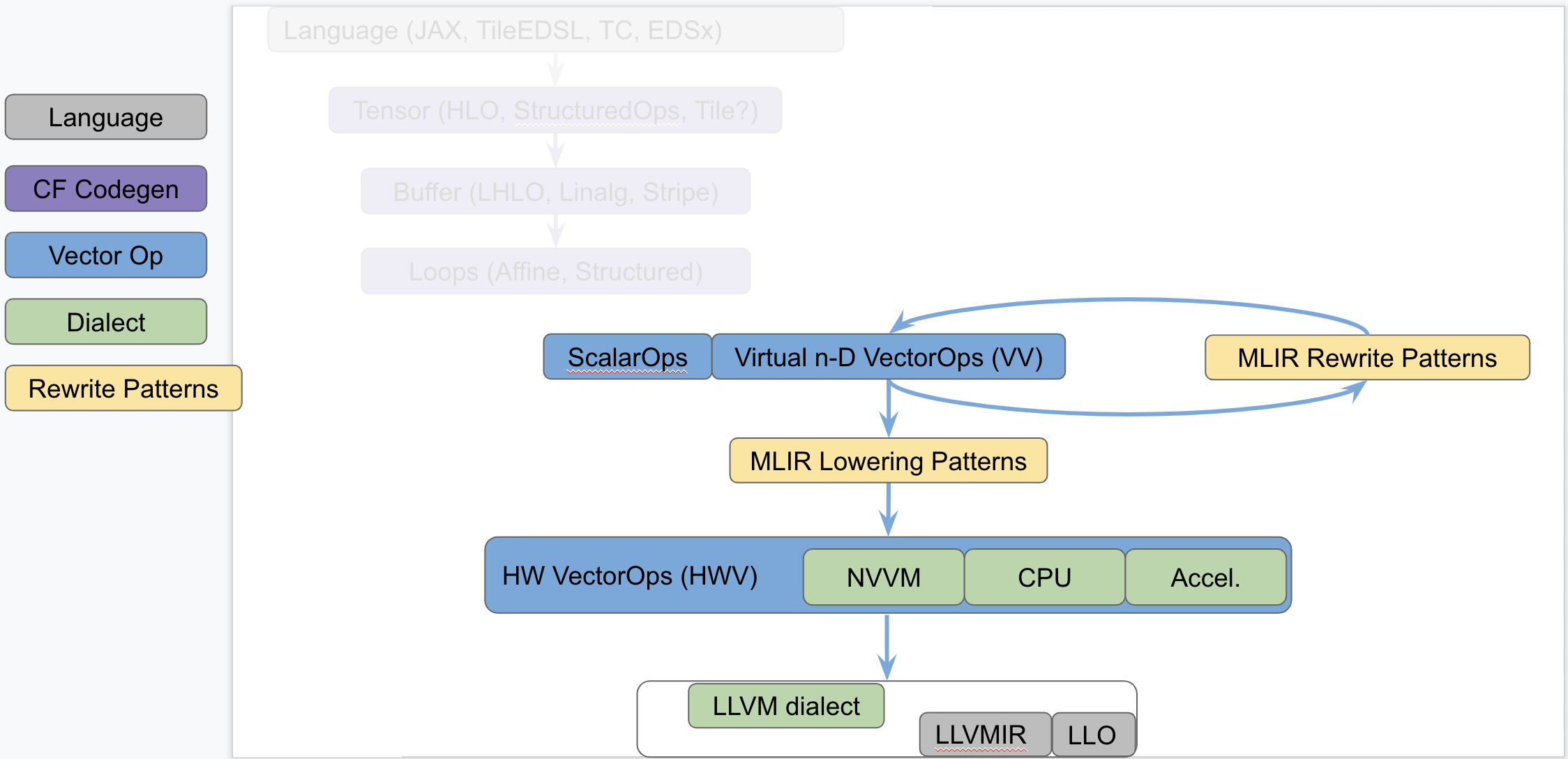
This separates concerns related to (a) defining efficient operations on
`vector` types from (b) program analyses + transformations on `memref`, loops
and other types of structured ops (be they `HLO`, `LHLO`, `Linalg` or other ).
Looking a bit forward in time, we can put a stake in the ground and venture that
the higher level of `vector`-level primitives we build and target from codegen
(or some user/language level), the simpler our task will be, the more complex
patterns can be expressed and the better performance will be.
## Components of a Generic Retargetable Vector-Level Dialect
The existing MLIR `vector`-level dialects are related to the following bottom-up
abstractions:
1. Representation in `LLVMIR` via data structures, instructions and intrinsics.
This is referred to as the `LLVM` level.
2. Set of machine-specific operations and types that are built to translate
almost 1-1 with the HW ISA. This is referred to as the Hardware Vector
level; a.k.a `HWV`. For instance, we have (a) the `NVVM` dialect (for
`CUDA`) with tensor core ops, (b) accelerator-specific dialects (internal),
a potential (future) `CPU` dialect to capture `LLVM` intrinsics more closely
and other dialects for specific hardware. Ideally this should be
auto-generated as much as possible from the `LLVM` level.
3. Set of virtual, machine-agnostic, operations that are informed by costs at
the `HWV`-level. This is referred to as the Virtual Vector level; a.k.a
`VV`. This is the level that higher-level abstractions (codegen, automatic
vectorization, potential vector language, ...) targets.
The existing generic, retargetable, `vector`-level dialect is related to the
following top-down rewrites and conversions:
1. MLIR Rewrite Patterns applied by the MLIR `PatternRewrite` infrastructure to
progressively lower to implementations that match closer and closer to the
`HWV`. Some patterns are "in-dialect" `VV -> VV` and some are conversions
`VV -> HWV`.
2. `Virtual Vector -> Hardware Vector` lowering is specified as a set of MLIR
lowering patterns that are specified manually for now.
3. `Hardware Vector -> LLVM` lowering is a mechanical process that is written
manually at the moment and that should be automated, following the `LLVM ->
Hardware Vector` ops generation as closely as possible.
## Short Description of the Existing Infrastructure
### LLVM level
On CPU, the `n-D` `vector` type currently lowers to `!llvm<array<vector>>`.
More concretely,
* `vector<4x8x128xf32>` lowers to `!llvm<[4 x [ 8 x < 128
x float >]]>` (fixed-width vector), and
* `vector<4x8x[128]xf32>` lowers to `!llvm<[4 x [ 8 x < vscale x 128
x float >]]>` (scalable vector).
There are tradeoffs involved related to how one can access subvectors and how
one uses `llvm.extractelement`, `llvm.insertelement` and `llvm.shufflevector`.
The section on [LLVM Lowering Tradeoffs](#llvm-lowering-tradeoffs) offers a
deeper dive into the current design choices and tradeoffs.
Note, while LLVM supports arrarys of scalable vectors, these are required to be
fixed-width arrays of 1-D scalable vectors. This means scalable vectors with a
non-trailing scalable dimension (e.g. `vector<4x[8]x128xf32`) are not
convertible to LLVM.
Finally, MLIR takes the same view on scalable Vectors as LLVM (c.f.
[VectorType](https://llvm.org/docs/LangRef.html#vector-type)):
> For scalable vectors, the total number of elements is a constant multiple
> (called vscale) of the specified number of elements; vscale is a positive
> integer that is unknown at compile time and the same hardware-dependent
> constant for all scalable vectors at run time. The size of a specific
> scalable vector type is thus constant within IR, even if the exact size in
> bytes cannot be determined until run time.
### Hardware Vector Ops
Hardware Vector Ops are implemented as one dialect per target. For internal
hardware, we are auto-generating the specific HW dialects. For `GPU`, the `NVVM`
dialect adds operations such as `mma.sync`, `shfl` and tests. For `CPU` things
are somewhat in-flight because the abstraction is close to `LLVMIR`. The jury is
still out on whether a generic `CPU` dialect is concretely needed, but it seems
reasonable to have the same levels of abstraction for all targets and perform
cost-based lowering decisions in MLIR even for `LLVM`. Specialized `CPU`
dialects that would capture specific features not well captured by LLVM peephole
optimizations of on different types that core MLIR supports (e.g. Scalable
Vectors) are welcome future extensions.
### Virtual Vector Ops
Some existing Arith and Vector Dialect on `n-D` `vector` types comprise:
```mlir
// Produces a vector<3x7x8xf32>
%a = arith.addf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%b = arith.mulf %0, %1 : vector<3x7x8xf32>
// Produces a vector<3x7x8xf32>
%c = vector.splat %1 : vector<3x7x8xf32>
%d = vector.extract %0[1]: vector<7x8xf32> from vector<3x7x8xf32>
%e = vector.extract %0[1, 5]: vector<8xf32> from vector<3x7x8xf32>
%f = vector.outerproduct %0, %1: vector<4xf32>, vector<8xf32> // -> vector<4x8xf32>
%g = vector.outerproduct %0, %1, %2: vector<4xf32>, vector<8xf32> // fma when adding %2
// Returns a slice of type vector<2x2x16xf32>
%h = vector.strided_slice %0
{offsets = [2, 2], sizes = [2, 2], strides = [1, 1]}:
vector<4x8x16xf32>
%i = vector.transfer_read %A[%0, %1]
{permutation_map = (d0, d1) -> (d0)}:
memref<7x?xf32>, vector<4xf32>
vector.transfer_write %f1, %A[%i0, %i1, %i2, %i3]
{permutation_map = (d0, d1, d2, d3) -> (d3, d1, d0)} :
vector<5x4x3xf32>, memref<?x?x?x?xf32>
```
The list of Vector is currently undergoing evolutions and is best kept track of
by following the evolution of the
[VectorOps.td](https://github.com/llvm/llvm-project/blob/main/mlir/include/mlir/Dialect/Vector/IR/VectorOps.td)
ODS file (markdown documentation is automatically generated locally when
building and populates the
[Vector doc](https://github.com/llvm/llvm-project/blob/main/mlir/docs/Dialects/Vector.md)).
Recent extensions are driven by concrete use cases of interest. A notable such
use case is the `vector.contract` op which applies principles of the
StructuredOps abstraction to `vector` types.
### Virtual Vector Rewrite Patterns
The following rewrite patterns exist at the `VV->VV` level:
1. The now retired `MaterializeVector` pass used to legalize ops on a
coarse-grained virtual `vector` to a finer-grained virtual `vector` by
unrolling. This has been rewritten as a retargetable unroll-and-jam pattern
on `vector` ops and `vector` types.
2. The lowering of `vector_transfer` ops legalizes `vector` load/store ops to
permuted loops over scalar load/stores. This should evolve to loops over
`vector` load/stores + `mask` operations as they become available `vector`
ops at the `VV` level.
The general direction is to add more Virtual Vector level ops and implement more
useful `VV -> VV` rewrites as composable patterns that the PatternRewrite
infrastructure can apply iteratively.
### Virtual Vector to Hardware Vector Lowering
For now, `VV -> HWV` are specified in C++ (see for instance the
[SplatOpLowering for n-D vectors](https://github.com/tensorflow/mlir/commit/0a0c4867c6a6fcb0a2f17ef26a791c1d551fe33d)
or the
[VectorOuterProductOp lowering](https://github.com/tensorflow/mlir/commit/957b1ca9680b4aacabb3a480fbc4ebd2506334b8)).
Simple
[conversion tests](https://github.com/llvm/llvm-project/blob/main/mlir/test/Conversion/VectorToLLVM/vector-to-llvm.mlir)
are available for the `LLVM` target starting from the Virtual Vector Level.
## Rationale
### Hardware as `vector` Machines of Minimum Granularity
Higher-dimensional `vector`s are ubiquitous in modern HPC hardware. One way to
think about Generic Retargetable `vector`-Level Dialect is that it operates on
`vector` types that are multiples of a "good" `vector` size so the HW can
efficiently implement a set of high-level primitives (e.g.
`vector<8x8x8x16xf32>` when HW `vector` size is say `vector<4x8xf32>`).
Some notable `vector` sizes of interest include:
1. CPU: `vector<HW_vector_size * k>`, `vector<core_count * k’ x
HW_vector_size * k>` and `vector<socket_count x core_count * k’ x
HW_vector_size * k>`
2. GPU: `vector<warp_size * k>`, `vector<warp_size * k x float4>` and
`vector<warp_size * k x 4 x 4 x 4>` for tensor_core sizes,
3. Other accelerators: n-D `vector` as first-class citizens in the HW.
Depending on the target, ops on sizes that are not multiples of the HW `vector`
size may either produce slow code (e.g. by going through `LLVM` legalization) or
may not legalize at all (e.g. some unsupported accelerator X combination of ops
and types).
### Transformations Problems Avoided
A `vector<16x32x64xf32>` virtual `vector` is a coarse-grained type that can be
“unrolled” to HW-specific sizes. The multi-dimensional unrolling factors are
carried in the IR by the `vector` type. After unrolling, traditional
instruction-level scheduling can be run.
The following key transformations (along with the supporting analyses and
structural constraints) are completely avoided by operating on a `vector`
`ssa-value` abstraction:
1. Loop unroll and unroll-and-jam.
2. Loop and load-store restructuring for register reuse.
3. Load to store forwarding and Mem2reg.
4. Coarsening (raising) from finer-grained `vector` form.
Note that “unrolling” in the context of `vector`s corresponds to partial loop
unroll-and-jam and not full unrolling. As a consequence this is expected to
compose with SW pipelining where applicable and does not result in ICache blow
up.
### The Big Out-Of-Scope Piece: Automatic Vectorization
One important piece not discussed here is automatic vectorization (automatically
raising from scalar to n-D `vector` ops and types). The TL;DR is that when the
first "super-vectorization" prototype was implemented, MLIR was nowhere near as
mature as it is today. As we continue building more abstractions in `VV -> HWV`,
there is an opportunity to revisit vectorization in MLIR.
Since this topic touches on codegen abstractions, it is technically out of the
scope of this survey document but there is a lot to discuss in light of
structured op type representations and how a vectorization transformation can be
reused across dialects. In particular, MLIR allows the definition of dialects at
arbitrary levels of granularity and lends itself favorably to progressive
lowering. The argument can be made that automatic vectorization on a loops + ops
abstraction is akin to raising structural information that has been lost.
Instead, it is possible to revisit vectorization as simple pattern rewrites,
provided the IR is in a suitable form. For instance, vectorizing a
`linalg.generic` op whose semantics match a `matmul` can be done
[quite easily with a pattern](https://github.com/tensorflow/mlir/commit/bff722d6b59ab99b998f0c2b9fccd0267d9f93b5).
In fact this pattern is trivial to generalize to any type of contraction when
targeting the `vector.contract` op, as well as to any field (`+/*`, `min/+`,
`max/+`, `or/and`, `logsumexp/+` ...) . In other words, by operating on a higher
level of generic abstractions than affine loops, non-trivial transformations
become significantly simpler and composable at a finer granularity.
Irrespective of the existence of an auto-vectorizer, one can build a notional
vector language based on the VectorOps dialect and build end-to-end models with
expressing `vector`s in the IR directly and simple pattern-rewrites.
[EDSC](https://github.com/llvm/llvm-project/blob/main/mlir/docs/EDSC.md)s
provide a simple way of driving such a notional language directly in C++.
## Bikeshed Naming Discussion
There are arguments against naming an n-D level of abstraction `vector` because
most people associate it with 1-D `vector`s. On the other hand, `vector`s are
first-class n-D values in MLIR. The alternative name Tile has been proposed,
which conveys higher-D meaning. But it also is one of the most overloaded terms
in compilers and hardware. For now, we generally use the `n-D` `vector` name and
are open to better suggestions.
## 0D Vectors
Vectors of dimension 0 (or _0-D vectors_ or _0D vectors_) are allowed inside
MLIR. For instance, a `f32` vector containing one scalar can be denoted as
`vector<f32>`. This is similar to the `tensor<f32>` type that is available in
TensorFlow or the `memref<f32>` type that is available in MLIR.
Generally, a 0D `vector` can be interpreted as a scalar. The benefit of 0D
`vector`s, `tensor`s, and `memref`s is that they make it easier to lower code
from various frontends such as TensorFlow and make it easier to handle corner
cases such as unrolling a loop from 1D to 0D.
## LLVM Lowering Tradeoffs
This section describes the tradeoffs involved in lowering the MLIR n-D vector
type and operations on it to LLVM-IR. Putting aside the
[LLVM Matrix](http://lists.llvm.org/pipermail/llvm-dev/2018-October/126871.html)
proposal for now, this assumes LLVM only has built-in support for 1-D vector.
The relationship with the LLVM Matrix proposal is discussed at the end of this
document.
LLVM instructions are prefixed by the `llvm.` dialect prefix (e.g.
`llvm.insertvalue`). Such ops operate exclusively on 1-D vectors and aggregates
following the [LLVM LangRef](https://llvm.org/docs/LangRef.html). MLIR
operations are prefixed by the `vector.` dialect prefix (e.g.
`vector.insertelement`). Such ops operate exclusively on MLIR `n-D` `vector`
types.
### Alternatives For Lowering an n-D Vector Type to LLVM
Consider a vector of rank n with static sizes `{s_0, ... s_{n-1}}` (i.e. an MLIR
`vector<s_0x...s_{n-1}xf32>`). Lowering such an `n-D` MLIR vector type to an
LLVM descriptor can be done by either:
1. Nested aggregate type of `1-D` vector:
`!llvm."[s_0x[s_1x[...<s_{n-1}xf32>]]]">` in the MLIR LLVM dialect (current
lowering in MLIR).
2. Flattening to a `1-D` vector: `!llvm<"(s_0*...*s_{n-1})xfloat">` in the MLIR
LLVM dialect.
3. A mix of both.
There are multiple tradeoffs involved in choosing one or the other that we
discuss. It is important to note that “a mix of both” immediately reduces to
“nested aggregate type of 1-D vector” with a `vector.cast %0:
vector<4x8x16x32xf32> to vector<4x4096xf32>` operation, that flattens the most
"k" minor dimensions.
### Constraints Inherited from LLVM (see LangRef)
The first constraint was already mentioned: LLVM only supports `1-D` `vector`
types natively. Additional constraints are related to the difference in LLVM
between vector and
[aggregate types](https://llvm.org/docs/LangRef.html#aggregate-types):
> Aggregate Types are a subset of derived types that can contain multiple
> member types. Arrays and structs are aggregate types. Vectors are not
> considered to be aggregate types.
This distinction is also reflected in some of the operations. For `1-D` vectors,
the operations `llvm.extractelement`, `llvm.insertelement`, and
`llvm.shufflevector` apply, with direct support for dynamic indices. For `n-D`
vectors with `n>1`, and thus aggregate types at LLVM level, the more restrictive
operations `llvm.extractvalue` and `llvm.insertvalue` apply, which only accept
static indices. There is no direct shuffling support for aggregate types.
The next sentence (cf. LangRef [structure
type](https://llvm.org/docs/LangRef.html#structure-type)) illustrates a
recurrent tradeoff, also found in MLIR, between
“value types” (subject to SSA use-def chains) and “memory types” (subject to
aliasing and side-effects):
> Structures in memory are accessed using ‘load’ and ‘store’ by getting a
> pointer to a field with the llvm.getelementptr instruction. Structures in
> registers are accessed using the llvm.extractvalue and llvm.insertvalue
> instructions.
When transposing this to MLIR, `llvm.getelementptr` works on pointers to `n-D`
vectors in memory. For `n-D`, vectors values that live in registers we can use
`vector.extract` and `vector.insert` which do not accept dynamic indices. Note
that this is consistent with hardware considerations as discussed below.
An alternative is to use an LLVM `1-D` `vector` type for which one can use
`llvm.extractelement`, `llvm.insertelement` and `llvm.shufflevector`. These
operations accept dynamic indices. The implication is that one has to use a
flattened lowering of an MLIR n-D vector to an LLVM 1-D vector.
There are multiple tradeoffs involved that mix implications on the programming
model, execution on actual HW and what is visible or hidden from codegen. They
are discussed in the following sections.
### Nested Aggregate
Pros:
1. Natural encoding n-D vector -> (n-1)-D aggregate over 1-D vector.
2. No need for linearization / delinearization logic inserted everywhere.
3. `llvm.insertvalue`, `llvm.extractvalue` of `(n-k)-D` aggregate is natural.
4. `llvm.insertelement`, `llvm.extractelement`, `llvm.shufflevector` over `1-D`
vector type is natural.
Cons:
1. `llvm.insertvalue` / `llvm.extractvalue` does not accept dynamic indices but
only static ones.
2. Dynamic indexing on the non-most-minor dimension requires roundtrips to
memory.
3. Special intrinsics and native instructions in LLVM operate on `1-D` vectors.
This is not expected to be a practical limitation thanks to a `vector.cast
%0: vector<4x8x16x32xf32> to vector<4x4096xf32>` operation, that flattens
the most minor dimensions (see the bigger picture in implications on
codegen).
### Flattened 1-D Vector Type
Pros:
1. `insertelement` / `extractelement` / `shufflevector` with dynamic indexing
is possible over the whole lowered `n-D` vector type.
2. Supports special intrinsics and native operations.
Cons:
1. Requires linearization/delinearization logic everywhere, translations are
complex.
2. Hides away the real HW structure behind dynamic indexing: at the end of the
day, HW vector sizes are generally fixed and multiple vectors will be needed
to hold a vector that is larger than the HW.
3. Unlikely peephole optimizations will result in good code: arbitrary dynamic
accesses, especially at HW vector boundaries unlikely to result in regular
patterns.
### Discussion
#### HW Vectors and Implications on the SW and the Programming Model
As of today, the LLVM model only support `1-D` vector types. This is
unsurprising because historically, the vast majority of HW only supports `1-D`
vector registers. We note that multiple HW vendors are in the process of
evolving to higher-dimensional physical vectors.
In the following discussion, let's assume the HW vector size is `1-D` and the SW
vector size is `n-D`, with `n >= 1`. The same discussion would apply with `2-D`
HW `vector` size and `n >= 2`. In this context, most HW exhibit a vector
register file. The number of such vectors is fixed. Depending on the rank and
sizes of the SW vector abstraction and the HW vector sizes and number of
registers, an `n-D` SW vector type may be materialized by a mix of multiple
`1-D` HW vector registers + memory locations at a given point in time.
The implication of the physical HW constraints on the programming model are that
one cannot index dynamically across hardware registers: a register file can
generally not be indexed dynamically. This is because the register number is
fixed and one either needs to unroll explicitly to obtain fixed register numbers
or go through memory. This is a constraint familiar to CUDA programmers: when
declaring a `private float a[4]`; and subsequently indexing with a *dynamic*
value results in so-called **local memory** usage (i.e. roundtripping to
memory).
#### Implication on codegen
MLIR `n-D` vector types are currently represented as `(n-1)-D` arrays of `1-D`
vectors when lowered to LLVM. This introduces the consequences on static vs
dynamic indexing discussed previously: `extractelement`, `insertelement` and
`shufflevector` on `n-D` vectors in MLIR only support static indices. Dynamic
indices are only supported on the most minor `1-D` vector but not the outer
`(n-1)-D`. For other cases, explicit load / stores are required.
The implications on codegen are as follows:
1. Loops around `vector` values are indirect addressing of vector values, they
must operate on explicit load / store operations over `n-D` vector types.
2. Once an `n-D` `vector` type is loaded into an SSA value (that may or may not
live in `n` registers, with or without spilling, when eventually lowered),
it may be unrolled to smaller `k-D` `vector` types and operations that
correspond to the HW. This level of MLIR codegen is related to register
allocation and spilling that occur much later in the LLVM pipeline.
3. HW may support >1-D vectors with intrinsics for indirect addressing within
these vectors. These can be targeted thanks to explicit `vector_cast`
operations from MLIR `k-D` vector types and operations to LLVM `1-D`
vectors + intrinsics.
Alternatively, we argue that directly lowering to a linearized abstraction hides
away the codegen complexities related to memory accesses by giving a false
impression of magical dynamic indexing across registers. Instead we prefer to
make those very explicit in MLIR and allow codegen to explore tradeoffs.
Different HW will require different tradeoffs in the sizes involved in steps 1.,
2. and 3.
Decisions made at the MLIR level will have implications at a much later stage in
LLVM (after register allocation). We do not envision to expose concerns related
to modeling of register allocation and spilling to MLIR explicitly. Instead,
each target will expose a set of "good" target operations and `n-D` vector
types, associated with costs that `PatterRewriters` at the MLIR level will be
able to target. Such costs at the MLIR level will be abstract and used for
ranking, not for accurate performance modeling. In the future such costs will be
learned.
#### Implication on Lowering to Accelerators
To target accelerators that support higher dimensional vectors natively, we can
start from either `1-D` or `n-D` vectors in MLIR and use `vector.cast` to
flatten the most minor dimensions to `1-D` `vector<Kxf32>` where `K` is an
appropriate constant. Then, the existing lowering to LLVM-IR immediately
applies, with extensions for accelerator-specific intrinsics.
It is the role of an Accelerator-specific vector dialect (see codegen flow in
the figure above) to lower the `vector.cast`. Accelerator -> LLVM lowering would
then consist of a bunch of `Accelerator -> Accelerator` rewrites to perform the
casts composed with `Accelerator -> LLVM` conversions + intrinsics that operate
on `1-D` `vector<Kxf32>`.
Some of those rewrites may need extra handling, especially if a reduction is
involved. For example, `vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32>`
when `K != K1 * … * Kn` and some arbitrary irregular `vector.cast %0:
vector<4x4x17xf32> to vector<Kxf32>` may introduce masking and intra-vector
shuffling that may not be worthwhile or even feasible, i.e. infinite cost.
However `vector.cast %0: vector<K1x...xKnxf32> to vector<Kxf32>` when `K = K1 *
… * Kn` should be close to a noop.
As we start building accelerator-specific abstractions, we hope to achieve
retargetable codegen: the same infra is used for CPU, GPU and accelerators with
extra MLIR patterns and costs.
#### Implication on calling external functions that operate on vectors
It is possible (likely) that we additionally need to linearize when calling an
external function.
### Relationship to LLVM matrix type proposal.
The LLVM matrix proposal was formulated 1 year ago but seemed to be somewhat
stalled until recently. In its current form, it is limited to 2-D matrix types
and operations are implemented with LLVM intrinsics. In contrast, MLIR sits at a
higher level of abstraction and allows the lowering of generic operations on
generic n-D vector types from MLIR to aggregates of 1-D LLVM vectors. In the
future, it could make sense to lower to the LLVM matrix abstraction also for CPU
even though MLIR will continue needing higher level abstractions.
On the other hand, one should note that as MLIR is moving to LLVM, this document
could become the unifying abstraction that people should target for 1-D vectors
and the LLVM matrix proposal can be viewed as a subset of this work.
### Conclusion
The flattened 1-D vector design in the LLVM matrix proposal is good in a
HW-specific world with special intrinsics. This is a good abstraction for
register allocation, Instruction-Level-Parallelism and
SoftWare-Pipelining/Modulo Scheduling optimizations at the register level.
However MLIR codegen operates at a higher level of abstraction where we want to
target operations on coarser-grained vectors than the HW size and on which
unroll-and-jam is applied and patterns across multiple HW vectors can be
matched.
This makes “nested aggregate type of 1-D vector” an appealing abstraction for
lowering from MLIR because:
1. it does not hide complexity related to the buffer vs value semantics and the
memory subsystem and
2. it does not rely on LLVM to magically make all the things work from a too
low-level abstraction.
The use of special intrinsics in a `1-D` LLVM world is still available thanks to
an explicit `vector.cast` op.
## Operations
[include "Dialects/VectorOps.md"]
Codebase Browser
llvm